CAST: CAD for Security and Trust

Description:

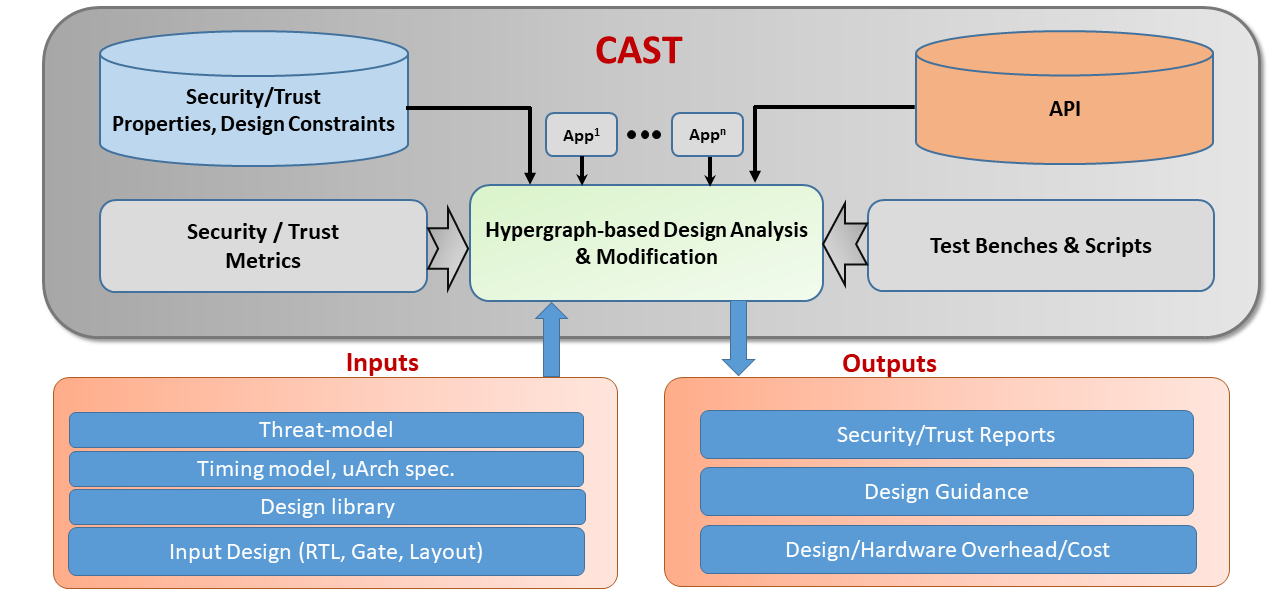
CAST stands for CAD for Security and Trust – it is a common development platform for diverse CAD tools towards automating the design/verification process for secure and trustworthy microelectronics. The critical technical piece of the framework is called NEOS (for “Netlist Encryption and Obfuscation Suit”) developed originally by Kaveh Shamsi. The tool has been under active development for over the last seven years. It was originally developed for research on gate-level hardware obfuscation defenses and attacks, hence the name “NEOS”). However, over the years additional features were added to the tool as discussed below, which resulted in a powerful, configurable framework for hardware security design and evaluation. It has been released under an open source license for several years. The tool has been used by various research groups in the hardware security area.

CAST provides a flexible, easy-to-use platform that can be used to develop new CAD tools for security and trust.

The API provides a large number of common functions in the following categories:

• Language The tool was developed using C++ from the ground up. The framework follows modern C++ conventions, including: (a) minimal use of raw C-style pointers and use of C++ smart-pointers instead; (b) object-oriented design through the usage of hierarchical classes for various tasks; (c) Use of std::any and std::variant for managing dynamic or multi-typed objects.
  
  
• Front-End: The tool consists of a set of front-end parsers. These parsers were originally custom hand-written loops. They were then reimplemented in the boost::spirit framework, and eventually reimplemented using the Lex/Bison automatic parser generator framework which provided more versatility and grammar expressiveness. These parsers can currently read gate-level designs in the .bench format, and gate-level Verilog (a subset of Verilog that includes only primitive gate functions and module instances). Additionally, the tool has parsers for reading .lib (Liberty) format cell libraries, Boolean expressions, and .genlib library formats. These allow for reading in cell libraries along with their Boolean functions and area/power/delay data.
  
  
• Circuit Representations and Algorithms: The framework can then represent designs read through the various front-ends to a couple of primary internal objects (C++ classes). First is the Cir class, which can represent bit-level circuits comprised of primitive gates or of cells/modules. In addition to the Cir object, there is an Aig object which represents And-Inverter-Graphs (AIGs). These are circuits that are comprised of 2-input AND gates with two masks that indicate whether the inputs are to be inverted or not. This format is used heavily in the ABC tool and other formal/circuit tools. Objects represented in the above two formats support a wide array of operations through the tool’s API. This includes various graph algorithms such as topological sorting, finding k-cuts, breadth/depth-first exploration, strongly-connected components, transitive fanin/fanout, trimming, and so on. Both objects support simulation of the circuit for both combinational and sequential circuits based on provided Boolean user input patterns. n-bit Boolean vectors can be simulated as well, which reduce to bit-parallel simulation of n different input patterns with one function call. A statistical module is available that can calculate signal probabilities using several approaches including, gate-level probability propagation, simulation-based , Binary-Decision-Diagram (BDD)-based, and combinations of the above . Circuits objects can also be converted to BDD objects interfacing to the cudd library. The user can limit the size of the BDD such that exploding BDDs are detected and avoided. These BDD representations can support some quantified Boolean formula (QBF) procedures. Finally, a set of circuit simplification algorithms is also integrated. These include simulation+SAT-based simplification of circuits and AIGs , BDD-based simplification, and ZDD-based simplification and also local rewriting-based simplification, are implemented. A technology mapper is also available which can do area-reduction-greedy mapping of AIGs to standard-cell libraries.
  
  
• Logic Obfuscation/Deobfuscation Engine: A wide array of circuit obfuscation and logic locking algorithms are implemented. These include traditional locking schemes such as random gate insertion, \eg,. XOR/XNOR , LUT , AND/OR , MUX insertion, to more recent point-function and cyclic obfuscation schemes. Furthermore, a wide array of circuit learning algorithms are implemented. These include the well-known SAT-based deobfuscation algorithm and a dozen variants. These algorithms are based on using the SAT interface to find input patterns, querying which will help disqualify incorrect keys iteratively, until the correct key/completion k* is found. In addition, a set of statistical deobfuscation algorithms are also implemented. These are based on using Boolean optimization algorithms to find keys that minimize the disagreement between the oracle and the hypothesized keyed circuit.
  
  
• Integration with Formal Tools. Formal circuit analysis is enabled by a set of interfaces and algorithms. Converting circuits to conjunctive-normal-formal (CNF) formulae and interfaces to Boolean satisfiability solvers (Glucouse, Minisat, CryptoMinisat) and satisfiability-modulo theories (SMT)-Solvers are provided. These can allow for various formal analysis tasks such as formal equivalence checking, Circuit-SAT and so on.
  
  
• Circuit Learning/Deobfuscation Engine: Given a circuit C(k, x) with a controllable input vector x and an unknown vector k, the task of finding the value of k* such that C(k*, x) and Co(x) become equivalent is the circuit deobfuscation or learning problem. In case it is possible to make queries to a black-box that implements Co, this is called oracle-guided circuit deobfuscation. The tool implements a wide array of circuit learning algorithms. These include the well-known SAT-based deobfuscation algorithm and a dozen variants. These algorithms are based on using the SAT interface to find input patterns, querying which will help disqualify incorrect keys iteratively, until the correct key/completion k* is found. SAT-based deobfuscation variants include approximate SAT-based deobfuscation, k-DIP, etc. In addition to SAT-based deobfuscation, a set of statistical deobfuscation algorithms are also implemented. These are based on using Boolean optimization algorithms to find keys that minimize the disagreement between the oracle and the hypothesizes keyed circuit.
  
  
• Statistical Optimizers. An array of Boolean optimizers is implemented that take in a user-defined cost function that is minimized through making changes to a Boolean solution vector. Simulated annealing, the genetic algorithms, and tree-based exploration, are implemented and can be used in various tasks. For instance, they can be used for implementing circuit deobfsucation algorithms, and side-channel analysis algorithms. Additionally, a back-propagation based statistical optimizer is implemented which can optimize a Boolean circuit condition using an analog of the back-propagation algorithm used to optimize neural networks.
  
  
• Side-Channel Analysis. An array of side-channel analysis routines has been implemented and integrated into the framework. These include a set of trace-collectors such as hamming-weight-based trace simulation, spice circuit-simulation based trace generation, and external oscilloscope trace collection. Currently PicoScope and Visa (KeySight) devices are supported. Once traces are collected they can be stored in a Trace_DB database. The database has built in serialization/deserialization support using the boost::serialization library. Furthermore, side channel algorithms have been implemented using the armadillo algebra library. These include correlation power analysis (CPA), differential power analysis (DPA), template analysis , and machine-learning based analysis using an interface to mlpack.
  
  
• Algebraic System A system for converting circuits to their polynomial representation in GF(2) is implemented. This is known as the algebraic normal form (ANF) which, similar to BDDs, is a canonical representation of the circuit’s functionality and can be used for formal tasks. Additionally, there is zero-suppressed binary decision diagram (ZDD)-based representation of ANF polynomials which can exponentially reduce the size of the representation.
  
  
• Circuit Simplification:  The frameowork implements a set of circuit simplification algorithms. These are critical in formal analysis tasks, as simplification of circuits results in the simplication of formal conditions and faster SAT/BDD runtimes. These include simulation+SAT-based simplification of circuits and AIGs, BDD-based simplification, and ZDD-based simplification, and also local rewriting-based simplification, are implemented. A technology mapper is also available which can do area-reduction-greedy mapping of AIGs to standard-cell libraries.
  
  
• Performance: The tool was implemented with the goal of scalability and performance from the ground up. At the time of this writing the artifact was the fastest SAT-based circuit deobfuscation tool. On side channel analysis, it beats existing Python-based implementations such as those provided by the ChipWhisperer library. The reason for this high performance is primarily due to (1) implementation in a fast compiled language (c++), (2) a custom utl::idmap data-structure used instead of traditional Hash/tree-map data-structure which has access runtime similar to that of std::vector (normal arrays); and (3) the combination of circuit simplification with advanced formal tools.

Developers:

• Kaveh Shamsi, University of Texas at Dallas
• Yier Jin, University of Florida
• Sandip Ray, University of Florida
• Tamzidul Hoque, University of Kansas
• Prabuddha Chakraborty, University of Maine
• Swarup Bhunia, University of Florida

Contact:

• Kaveh Shamsi
• Sandip Ray
• Tamzidul Hoque
• Prabuddha Chakraborty

References

@inproceedings{Shamsi2019c,

title = {IcySAT: Improved SAT-based Attacks on Cyclic Locked Circuits},

author = {Kaveh Shamsi and David Z. Pan and Yier Jin},

url = {http://cadforassurance.org/wp-content/uploads/IcySAT.pdf},

doi = {10.1109/ICCAD45719.2019.8942049},

year  = {2019},

date = {2019-11-05},

booktitle = {2019 IEEE/ACM International Conference on Computer-Aided Design (ICCAD)},

pages = {1-7},

publisher = {IEEE},

abstract = {“Cyclic” circuit locking/camouflaging is a recently proposed direction in logic obfuscation for thwarting foundry and end-user reverse engineering. As opposed to traditional schemes, these techniques create cycles in the obfuscated circuit in a way that confuses the attacker but does not disrupt the combinational nature of the circuit. While these schemes can thwart the baseline SAT-based attack, the CycSAT attack was proposed recently to break these schemes through a preprocessing step that builds a Boolean condition to avoid cyclic solutions/keys during the attack. However, follow-up work has suggested that extracting these conditions requires enumerating all cycles in the circuit, or that instead of relying on these conditions preemptively, cyclic solutions must be banned individually on the fly. In this paper, we present new algorithms for performing SAT-based attacks on cyclic circuits. We first propose an algorithm that can produce non-cyclic conditions in polynomial time with respect to the size of the circuit, avoiding the potentially exponential runtime of explicit key-banning or cycle enumeration. We then take a deeper look at the problem, discussing some of the fundamental limitations of extracting precise non-cyclic conditions and propose a more complex but complete procedure for cyclic deobfuscation. We evaluate our attacks on densely cyclic obfuscated benchmark circuits.},

keywords = {},

pubstate = {published},

tppubtype = {inproceedings}

}

@article{Shamsi2019d,

title = {IP Protection and Supply Chain Security through Logic Obfuscation: A Systematic Overview},

author = {Kaveh Shamsi and Meng Li and Kenneth Plaks and Saverio Fazzari and David Z. Pan and Yier Jin},

url = {http://cadforassurance.org/wp-content/uploads/kaveh2019ip.pdf},

doi = {10.1145/3342099},

year  = {2019},

date = {2019-09-01},

journal = {ACM Transactions on Design Automation of Electronic Systems (TODAES)},

volume = {24},

number = {6},

pages = {1-36},

abstract = {The globalization of the semiconductor supply chain introduces ever-increasing security and privacy risks. Two major concerns are IP theft through reverse engineering and malicious modification of the design. The latter concern in part relies on successful reverse engineering of the design as well. IC camouflaging and logic locking are two of the techniques under research that can thwart reverse engineering by end-users or foundries. However, developing low overhead locking/camouflaging schemes that can resist the ever-evolving state-of-the-art attacks has been a challenge for several years. This article provides a comprehensive review of the state of the art with respect to locking/camouflaging techniques. We start by defining a systematic threat model for these techniques and discuss how various real-world scenarios relate to each threat model. We then discuss the evolution of generic algorithmic attacks under each threat model eventually leading to the strongest existing attacks. The article then systematizes defenses and along the way discusses attacks that are more specific to certain kinds of locking/camouflaging. The article then concludes by discussing open problems and future directions.},

keywords = {},

pubstate = {published},

tppubtype = {article}

}

@article{Li2019,

title = {Provably Secure Camouflaging Strategy for IC Protection},

author = {Meng Li and Kaveh Shamsi and Travis Meade and Zheng Zhao and Bei Yu and Yier Jin and David Z. Pan },

url = {http://cadforassurance.org/wp-content/uploads/li2019provably.pdf},

doi = {10.1109/TCAD.2017.2750088},

year  = {2019},

date = {2019-08-03},

booktitle = {Provably Secure Camouflaging Strategy for IC Protection},

journal = {IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems},

volume = {38},

number = {8},

pages = {1399-1412},

abstract = {The advancing of reverse engineering techniques has complicated the efforts in intellectual property protection. Proactive methods have been developed recently, among which layout-level integrated circuit camouflaging is the leading example. However, existing camouflaging methods are rarely supported by provably secure criteria, which further leads to an over-estimation of the security level when countering the latest de-camouflaging attacks, e.g., the SAT-based attack. In this paper, a quantitative security criterion is proposed for de-camouflaging complexity measurements and formally analyzed through the demonstration of the equivalence between the existing de-camouflaging strategy and the active learning scheme. Supported by the new security criterion, two camouflaging techniques are proposed, including the low-overhead camouflaging cell generation strategy and the AND-tree camouflaging strategy, to help achieve exponentially increasing security levels at the cost of linearly increasing performance overhead on the circuit under protection. A provably secure camouflaging framework is then developed combining these two techniques. The experimental results using the security criterion show that camouflaged circuits with the proposed framework are of high resilience against different attack schemes with an only negligible performance overhead.},

keywords = {},

pubstate = {published},

tppubtype = {article}

}

@inproceedings{Shamsi2019b,

title = {On the Impossibility of Approximation-Resilient Circuit Locking},

author = {Kaveh Shamsi and David Z. Pan and Yier Jin},

url = {http://cadforassurance.org/wp-content/uploads/kaveh2019on.pdf},

doi = {10.1109/HST.2019.8741035},

year  = {2019},

date = {2019-05-06},

booktitle = {2019 IEEE International Symposium on Hardware Oriented Security and Trust (HOST)},

journal = {2019 IEEE International Symposium on Hardware Oriented Security and Trust (HOST)},

pages = {161-170},

abstract = {Logic locking, and Integrated Circuit (IC) Camouflaging, are techniques that try to hide the design of an IC from a malicious foundry or end-user by introducing ambiguity into the netlist of the circuit. While over the past decade an array of such techniques have been proposed, their security has been constantly challenged by algorithmic attacks. This may in part be due to a lack of formally defined notions of security in the first place, and hence a lack of security guarantees based on long-standing hardness assumptions. In this paper, we take a formal approach. We define the problem of circuit locking (cL) as transforming an original circuit to a locked one which is “unintelligible” without a secret key (this can model camouflaging and split-manufacturing in addition to logic locking). We define several notions of security for cL under different adversary models. Using long-standing results from computational learning theory we show the impossibility of exponentially approximation-resilient locking in the presence of an oracle for large classes of Boolean circuits. We then show how exact-recovery-resiliency and a more relaxed notion of security that we coin “best-possible” approximation-resiliency can be provably guaranteed with polynomial overhead. Our theoretical analysis directly results in stronger attacks and defenses which we demonstrate through experimental results on benchmark circuits.},

keywords = {},

pubstate = {published},

tppubtype = {inproceedings}

}

@article{Shamsi2019cb,

title = {On the Approximation Resiliency of Logic Locking and IC Camouflaging Schemes},

author = {Kaveh Shamsi and Travis Meade and Meng Li and David Z. Pan and Yier Jin},

url = {http://cadforassurance.org/wp-content/uploads/kaveh2019onappro.pdf},

doi = {10.1109/TIFS.2018.2850319},

year  = {2019},

date = {2019-02-01},

journal = {IEEE Transactions on Information Forensics and Security (TIFS)},

volume = {14},

number = {2},

pages = {347-359},

abstract = {The SAT-based attacks are extremely successful in deobfuscating the traditional combinational logic locking and IC camouflaging schemes. While several SAT-resilient protection schemes that increase the minimum query count of the attack have been proposed recently, none of them satisfy the output corruptibility (error) criteria. Therefore, most of them were combined with high corruptibility schemes to achieve both corruptibility and high query count. These “compound” schemes are successful since existing SAT attacks are agnostic to the corruptibility of the protection scheme. In this paper, we propose an approximate SAT-based attack framework that focuses on the iterative convergence of an attack toward a better solution. This helps our attack reduce a compound scheme to a standalone SAT-resilient scheme. In addition, we relate the problem of minimum query count to a well-known graph problem, and we propose a novel technique to increase the corruptibility of SAT-resilient protection schemes in a controllable manner. This creates protection schemes that have both high query count and corruptibility. Furthermore, due to the approximation resiliency property of these schemes, approximate attacks provide no advantage over exact attacks when attacking them.},

keywords = {},

pubstate = {published},

tppubtype = {article}

}